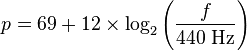DictionaryPitches |
| Buy sheetmusic at SheetMusicPlus |
|
Pitch represents the perceived fundamental frequency of a sound.[1] It is one of the major auditory attributes of musical tones along with duration, loudness, timbre, and sound source location. Pitch allows the construction of melodies; pitches are compared as "higher" and "lower", and are quantified as frequencies (cycles per second, or hertz), corresponding very nearly to the repetition rate of sound waves. However, pitch is not an objective physical property, but a subjective psychophysical attribute of sound.[2]
Perception of pitchPitch is a subjective sensation in which a listener assigns perceived tones to relative positions on a musical scale based primarily on the frequency of vibration. The just-noticeable difference (jnd, the threshold at which a change is perceived) depends on the tone's frequency and is about 4.3 cents (1 cent = 1 hundredth of a semitone) or about 0.36 Hz in frequency within the octave of 1,000–2,000 Hz but within the octave 62–125 Hz the jnd is much coarser with some 40 cents or about 2 Hz between perceived pitch changes. The jnd is typically tested by playing two tones in quick succession with the listener asked if there was a difference in their pitches.[3] The jnd becomes smaller if the two tones are played simultaneously as the listener is then able to discern beat frequencies. The total number of perceptible pitch steps in the range of human hearing is about 1,400; the total number of notes in the equal-tempered scale is 120.[3] Pitch is related to frequency, but they are not equivalent. Frequency is the scientific measure of pitch. While frequency is objective, pitch is completely subjective. The pitch of complex tones is ambiguous, meaning that two or more different pitches can be perceived depending upon the direction of attention of the observer.[4] Sound waves themselves do not have pitch; their oscillations can be measured to obtain a frequency, but it takes a human brain to map them to that internal quality of pitch. When the actual fundamental frequency can be precisely determined through physical measurement, it may differ from the perceived pitch because of overtones, also known as upper partials, harmonic or otherwise. The human auditory perception system may also have trouble distinguishing frequency differences between notes under certain circumstances. According to ANSI acoustical terminology, it is the auditory attribute of sound according to which sounds can be ordered on a scale from low to high. The relative perception of pitch can be fooled, resulting in "aural illusions". There are several of these, such as the tritone paradox, but most notably the Shepard scale, where a continuous or discrete sequence of specially formed tones can be made to sound as if the sequence continues ascending or descending forever. Pitch depends to lesser degree on the sound pressure level (loudness, volume) of the tone, especially at frequencies below 1,000 Hz and above 2,000 Hz. The pitch of lower tones gets lower as sound pressure increases. For instance, a tone of 200 Hz that is very loud will seem to be one semitone lower in pitch than if it is just barely audible. The pitch of higher tones gets higher as the sound gets louder.[3] Sounds more complex than a pure sine wave also have pitch, notably speech and musical notes. Many such sounds are approximately periodic, and the perceived pitch is directly related to the period. A complex tone composed of two sine waves of 1000 and 1200 Hz will have three pitches. Two spectral pitches at 1000 and 1200 Hz, derived from the physical frequencies of the pure tones; and one "virtual pitch" at 200 Hz, derived from the repetition rate of the waveform. They also have a spectrum that is (approximately) a stack of harmonics, and the perceived pitch is related to the harmonic spacing. The lowest harmonic in the stack is called the fundamental frequency, and its frequency is also strongly correlated with the pitch, though a strong pitch may be perceived even when the fundamental is missing. Historically, the study of pitch perception, and especially of pitch in the case of the missing fundamental, has been a central problem in psychoacoustics, and has been very instrumental in forming and testing theories of sound representation, processing, and perception in the auditory system.[5] Some theories of pitch perception hold that pitch has inherent octave ambiguities, and therefore is best decomposed into a pitch chroma, a periodic value around the octave, like the note names in western music, and a pitch height, which may be ambiguous, indicating which octave the pitch may be in.[5] Definite and indefinite pitchNot all musical instruments make notes with a clear pitch; percussion instruments are often distinguished by whether they do or do not have a particular pitch. A sound or note of definite pitch is one of which it is possible or relatively easy to discern the pitch. Sounds with definite pitch have harmonic frequency spectra or close to harmonic spectra.[3] A sound generated on any instrument produces many modes of vibration occurring simultaneously. A listener hears numerous frequencies at once. The vibration that has the slowest rate is called the fundamental frequency, the other frequencies are overtones.[6] An important class of overtones is formed by the harmonics, which have frequencies in integer multiples of the fundamental. A sound or note of indefinite pitch is one of which it is impossible or relatively difficult to discern a pitch. Sounds with indefinite pitch do not have harmonic spectra or have altered harmonic spectra. It is still possible for two sounds of indefinite pitch to clearly be higher or lower than one another, for instance, a snare drum invariably sounds higher in pitch than a bass drum, though both have indefinite pitch, because its sound contains higher frequencies. In other words, it is possible and often easy to roughly discern the relative pitches of two sounds of indefinite pitch, but any given sound of indefinite pitch does not neatly correspond to a given definite pitch. A special type of pitch often occurs in free nature when the sound of a sound source reaches the ear of an observer directly and also after being reflected against a sound-reflecting surface. This phenomenon is called repetition pitch, because the addition of a true repetition of the original sound to itself is the basic prerequisite. Concert pitchMain article: Concert pitch
Concert pitch is the pitch reference to which a group of musical instruments are tuned for a performance. Concert pitch may vary from ensemble to ensemble, and has varied widely over musical history. The A above middle C is usually set at 440 Hz (often written as "A = 440 Hz" or sometimes "A440"), although other frequencies are also often used, such as 442 Hz. Historically, this A has been tuned to a variety of higher and lower pitches. For example, Michael Praetorius proposed a standard of 465 Hz in the early 17th century.[7][not in citation given] The transposing instruments in an orchestra will conventionally have their parts transposed into different keys from the other instruments (and even from each other). As a result, musicians need a way to refer to a particular pitch in an unambiguous manner when talking to different sections of the orchestra. For example, the most common type of clarinet or trumpet, when playing a note written in their part as C, will sound a pitch that would be called B♭ on a non-transposing instrument like a piano. If you wanted to refer to that pitch unambiguously, you would call it "concert B♭", meaning "the pitch that someone playing a non-transposing instrument like a piano would call B♭". Labeling pitches
Note frequencies, four-octave C major diatonic scale, starting with C1.
Pitches can be labeled using letters, as in Helmholtz pitch notation, using a combination of letters and numbers, as in scientific pitch notation, or by a number representing frequency. For example, one might refer to the A above middle C as "a'", "A4" or "A440". In standard Western equal temperament, the notion of pitch is insensitive to spelling: the description "G4 double sharp" refers to the same pitch as "A4". Human pitch perception is approximately logarithmic with respect to fundamental frequency: the perceived distance between the pitches "A220" and "A440" is the same as the perceived distance between the pitches "A440" and "A880." Motivated by this logarithmic perception, music theorists sometimes represent pitches using a numerical scale based on the logarithm of fundamental frequency. For example, one can adopt the widely used MIDI standard to map fundamental frequency f to a real number p as follows This creates a linear pitch space in which octaves have size 12, semitones (the distance between adjacent keys on the piano keyboard) have size 1, and A440 is assigned the number 69. Distance in this space corresponds to musical distance as measured in psychological experiments and understood by musicians. (An equal-tempered semitone is subdivided into 100 cents.) The system is flexible enough to include "microtones" not found on standard piano keyboards. For example, the pitch halfway between C (60) and C♯ (61) can be labeled 60.5. ScalesThe relative pitches of individual notes in a scale may be determined by one of a number of tuning systems. In the west, the twelve-note chromatic scale is the most common method of organization, with equal temperament now the most widely used method of tuning that scale. In it, the pitch ratio between any two successive notes of the scale is exactly the twelfth root of two (or about 1.05946). In well-tempered systems (as used in the time of Johann Sebastian Bach, for example), different methods of musical tuning were used. Almost all of these systems have one interval in common, the octave, where the pitch of one note is double the frequency of another. For example, if the A above middle C is 440 Hz, the A an octave above that will be 880 Hz . Other musical meanings of pitchIn atonal, twelve tone, or musical set theory a "pitch" is a specific frequency while a pitch class is all the octaves of a frequency. Pitches are named with integers because of octave and enharmonic equivalency (for example, C♯ and D♭ are the same pitch, while C4 and C5 are functionally the same, one octave apart). Discrete pitches, rather than continuously variable pitches, are virtually universal, with exceptions including "tumbling strains" [8] and "indeterminate-pitch chants".[9] Gliding pitches are used in most cultures, but are related to the discrete pitches they reference or embellish.[10] Changing the pitch of a vibrating stringThere are three ways to change the pitch of a vibrating string. String instruments are tuned by varying the strings' tension because adjusting length or mass per unit length is impractical. Instruments with a fingerboard are then played by adjusting the length of the vibrating portion of the strings. LengthPitch can be adjusted by varying the length of the string. A longer string will result in a lower pitch, while a shorter string will result in a higher pitch. The frequency is inversely proportional to the length: A string twice as long will produce a tone of half the frequency (one octave lower). TensionPitch can be adjusted by varying the tension of the string. A string with less tension (looser) will result in a lower pitch, while a string with greater tension (tighter) will result in a higher pitch. The frequency is proportional to the square root of the tension: DensityThe pitch of a string can also be varied by changing the density of the string. The frequency is inversely proportional to the square root of the density: A string that is denser will produce a lower pitch. See also
References
Further reading
External links
| |||||||||||||||||||||||
This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Pitches". Allthough most Wikipedia articles provide accurate information accuracy can not be guaranteed. | |||||||||||||||||||||||
Help us with donations or by making music available!
©2023 Classic Cat - the classical music directory

Liszt, F.
Ballade no. 2
Dorian Griner
Bach, J.S.
Cello Suite No. 1 in G major
Marcin Masecki
Schubert, F.
Symphony No. 8 in B minor "Unfinished"
Berliner Philharmoniker
Chopin, F.
12 Etudes Op. 10
Washington Musica Viva
Satie, E.
Chapitres tournes en tous sens
Francois de Larrard
Beethoven, L. van
Octet for Oboes, Clarinets, Horns & Bassoons
Soni Ventorum Wind Quintet