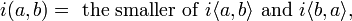In musical set theory, an interval class (often abbreviated: ic), also known as unordered pitch-class interval, interval distance, undirected interval, or (completely incorrectly, since this would mean, e.g., that a perfect fourth and a minor second are inversionally equivalent and belong to the same interval class, as would a unison and a tritone) interval mod 6 (Rahn 1980, 29; Whittall 2008, 273–74), is the shortest distance in pitch class space between two unordered pitch classes. For example, the interval class between pitch classes 4 and 9 is 5 because 9 − 4 = 5 is less than 4 − 9 = −5 ≡ 7 (mod 12). See modular arithmetic for more on modulo 12. The largest interval class is 6 since any greater interval n may be reduced to 12 − n.

Use of interval classes

The concept of interval class was created to account for octave, enharmonic, and inversional equivalency.^{[original research?]} Consider, for instance, the following passage:

(To hear a MIDI realization, click the following: 106 KB (help·info)

In the example above, all four labeled pitch-pairs, or dyads, share a common "intervallic color." In atonal theory, this similarity is denoted by interval class—ic 5, in this case. Tonal theory, however, classifies the four intervals differently: interval 1 as perfect fifth; 2, perfect twelfth; 3, diminished sixth; and 4, perfect fourth. Thus we see that in a dodecaphonic (i.e., chromatic) context, terminology tailored for the analysis of heptatonic (i.e., diatonic) music is often no longer suitable.^{[original research?]}

Incidentally, the example's pitch collection forms an octatonic set.^{[original research?]}

Notation of interval classes

The unordered pitch class interval i (a, b) may be defined as

where i <a, b> is an ordered pitch class interval (Rahn 1980, 28).

While notating unordered intervals with parentheses, as in the example directly above, is perhaps the standard, some theorists, including Robert Morris (1991), prefer to use braces, as in i {a,b}. Both notations are considered acceptable.

Table of interval class equivalencies

Sources

• Morris, Robert (1991). Class Notes for Atonal Music Theory. Hanover, NH: Frog Peak Music.
• Rahn, John (1980). Basic Atonal Theory. ISBN 0-02-873160-3. For forumala definitions only.
• Whittall, Arnold (2008). The Cambridge Introduction to Serialism. New York: Cambridge University Press. ISBN 978-0-521-68200-8 (pbk).

Further reading

• Friedmann, Michael (1990). Ear Training for Twentieth-Century Music. New Haven: Yale University Press. ISBN 0-300-04536-0 (cloth) ISBN 0-300-04537-9 (pbk)

External links

• Solomon's Set Theory Primer