DictionarySet_theory |
| Buy sheetmusic at SheetMusicPlus |

Example of Z-relation on two pitch sets analyzable as or derivable from Z17 (Schuijer 2008, p.99), with intervals between pitch classes labeled for ease of comparison between the two sets and their common interval vector, 212320.
Musical set theory provides concepts for categorizing musical objects and describing their relationships. Many of the notions were first elaborated by Howard Hanson (1960) in connection with tonal music, and then mostly developed in connection with atonal music by theorists such as Allen Forte (1973), drawing on the work in twelve-tone theory of Milton Babbitt. The concepts of set theory are very general and can be applied to tonal and atonal styles in any equally-tempered tuning system, and to some extent more generally than that. Musical set theory deals with collections (set (music) and permutation (music)) of pitches and pitch classes, which may be ordered or unordered (order (mathematics)), and which can be related by musical operations such as transposition, inversion, and complementation. The methods of musical set theory are sometimes applied to the analysis of rhythm as well.
Mathematical set theory versus musical set theoryAlthough musical set theory is often thought to involve the application of mathematical set theory to music, there are numerous differences between the methods and terminology of the two. For example, musicians use the terms transposition and inversion where mathematicians would use translation and reflection. Furthermore, musicians talk about "ordered sets" where mathematicians would talk about permutations, sequences or tuples. Moreover, musical set theory is more closely related to group theory and combinatorics than to mathematical set theory, which concerns itself with such matters as, for example, various sizes of infinitely large sets. In combinatorics, an unordered subset of n objects, such as pitch classes, is called a combination, and an ordered subset a permutation. Musical set theory is best regarded as a field that is not so much related to mathematical set theory, as an application of combinatorics to music theory with its own vocabulary. The main connection to mathematical set theory is the use of the vocabulary of set theory to talk about finite sets. Set and set typesMain article: Set (music)
The fundamental concept of musical set theory is the (musical) set, which is an unordered collection of pitch classes (Rahn 1980, 27). More exactly, a pitch-class set is a numerical representation consisting of distinct integers (i.e., without duplicates) (Forte 1973, 3). The elements of a set may be manifested in music as simultaneous chords, successive tones (as in a melody), or both.[citation needed] Notational conventions vary from author to author, but sets are typically enclosed in curly braces: {} (Rahn 1980, 28), or square brackets:[] (Forte 1973, 3). Some theorists use angle brackets Though set theorists usually consider sets of equal-tempered pitch classes, it is possible to consider sets of pitches, non-equal-tempered pitch classes,[citation needed] rhythmic onsets, or "beat classes" (Warburton 1988, 148; Cohn 1992, 149). Two-element sets are called dyads, three-element sets trichords (occasionally triads, though this is easily confused with the traditional meaning of the word). Sets of higher cardinalities are called tetrachords (or tetrads), pentachords (or pentads), hexachords (or hexads), heptachords (heptads or, sometimes, mixing Latin and Greek roots, "septachords"—e.g., Rahn 1980, 140), octachords (octads), nonachords (nonads), decachords (decads), undecachords, and, finally, the dodecachord. Basic operationsThe basic operations that may be performed on a set are transposition and inversion. Sets related by transposition or inversion are said to be transpositionally related or inversionally related, and to belong to the same set class. Since transposition and inversion are isometries of pitch-class space, they preserve the intervallic structure of a set, and hence its musical character. This can be considered the central postulate of musical set theory. In practice, set-theoretic musical analysis often consists in the identification of non-obvious transpositional or inversional relationships between sets found in a piece. Some authors consider the operations of complementation and multiplication as well. (The complement of set X is the set consisting of all the pitch classes not contained in X (Forte 1973, 73–74).) However, since complementation and multiplication are not isometries of pitch-class space, they do not necessarily preserve the musical character of the objects they transform. Other writers, such as Allen Forte, have emphasized the Z-relation which obtains between two sets sharing the same total interval content, or interval vector, but which are not transpositionally or inversionally equivalent (Forte 1973, 21). Another name for this relationship, used by Howard Hanson (1960), is "isomeric" (Cohen 2004, 33). Operations on ordered sequences of pitch classes also include transposition and inversion, as well as retrograde and rotation. Retrograding an ordered sequence reverses the order of its elements. Rotation of an ordered sequence is equivalent to cyclic permutation. Transposition and inversion can be represented as elementary arithmetic operations. If x is a number representing a pitch class, its transposition by n semitones is written Tn = x + n (mod12). Inversion corresponds to reflection around some fixed point in pitch class space. If "x" is a pitch class, the inversion with index number n is written In = n - x (mod12). Equivalence relation"For a relation in set S to be an equivalence relation [in algebra], it has to satisfy three conditions: it has to be reflexive [...], symmetrical [...], and transitive [...]."(Schuijer 2008, p.29-30) "Indeed, an informal notion of equivalence has always been part of music theory and analysis. PC set theory, however, has adhered to formal definitions of equivalence."(Schuijer 2008, p.85) Transpositional and inversional set classesTwo transpositionally related sets are said to belong to the same transpositional set class (Tn). Two sets related by transposition or inversion are said to belong to the same transpositional/inversional set class (inversion being written TnI or In). Sets belonging to the same transpositional set class are very similar-sounding; while sets belonging to the same transpositional/inversional set class are fairly similar sounding. Because of this, music theorists often consider set classes to be basic objects of musical interest. There are two main conventions for naming equal-tempered set classes. One, known as the Forte number, derives from Allen Forte, whose The Structure of Atonal Music (1973), is one of the first works in musical set theory. Forte provided each set class with a number of the form c-d, where c indicates the cardinality of the set and d is the ordinal number (Forte 1973, 12). Thus the chromatic trichord {0, 1, 2} belongs to set-class 3-1, indicating that it is the first three-note set class in Forte's list (Forte 1973, 179–81). The augmented trichord {0, 4, 8}, receives the label 3-12, which happens to be the last trichord in Forte's list. The primary criticisms of Forte's nomenclature are: (1) Forte's labels are arbitrary and difficult to memorize, and it is in practice often easier simply to list an element of the set class; (2) Forte's system assumes equal temperament and cannot easily be extended to include diatonic sets, pitch sets (as opposed to pitch-class sets), multisets or sets in other tuning systems; (3) Forte's original system considers inversionally related sets to belong to the same set-class.This means that, for example a major triad and a minor triad are considered the same set. Western tonal music for centuries has regarded major and minor as significantly different. Therefore there is a limitation in Forte's theory.[citation needed] However, the theory was not created to fill a vacuum in which existing theories inadequately explained tonal music. Rather, Forte's theory is used to explain atonal music, where the composer has invented a system where the distinction between {0, 4, 7} (called 'major' in tonal theory) and its inversion {0, 8, 5} (called 'minor' in tonal theory) may not be relevant. The second notational system labels sets in terms of their normal form, which depends on the concept of normal order. To put a set in normal order, order it as an ascending scale in pitch-class space that spans less than an octave. Then permute it cyclically until its first and last notes are as close together as possible. In the case of ties, minimize the distance between the first and next-to-last note. (In case of ties here, minimize the distance between the first and next-to-next-to-last note, and so on.) Thus {0, 7, 4} in normal order is {0, 4, 7}, while {0, 2, 10} in normal order is {10, 0, 2}. To put a set in normal form, begin by putting it in normal order, and then transpose it so that its first pitch class is 0 (Rahn 1980, 33–38). Mathematicians and computer scientists most often order combinations using either alphabetical ordering, binary (base two) ordering, or Gray coding, each of which lead to differing but logical normal forms.[citation needed] Since transpositionally related sets share the same normal form, normal forms can be used to label the Tn set classes. To identify a set's Tn/In set class:
The resulting set labels the initial set's Tn/In set class. SymmetryThe number of distinct operations in a system that map a set into itself is the set's degree of symmetry (Rahn 1980, 90). Every set has at least one symmetry, as it maps onto itself under the identity operation T0 (Rahn 1980, 91). Transpositionally symmetric sets map onto themselves for Tn where n does not equal 0. Inversionally symmetric sets map onto themselves under TnI. For any given Tn/TnI type all sets will have the same degree of symmetry. The number of distinct sets in a type is 24 (the total number of operations, transposition and inversion, for n = 0 through 11) divided by the degree of symmetry of Tn/TnI type. Transpositionally symmetrical sets either divide the octave evenly, or can be written as the union of equally-sized sets that themselves divide the octave evenly. Inversionally-symmetrical chords are invariant under reflections in pitch class space. This means that the chords can be ordered cyclically so that the series of intervals between successive notes is the same read forward or backward. For instance, in the cyclical ordering (0, 1, 2, 7), the interval between the first and second note is 1, the interval between the second and third note is 1, the interval between the third and fourth note is 5, and the interval between the fourth note and the first note is 5. One obtains the same sequence if one starts with the third element of the series and moves backward: the interval between the third element of the series and the second is 1; the interval between the second element of the series and the first is 1; the interval between the first element of the series and the fourth is 5; and the interval between the last element of the series and the third element is 5. Symmetry is therefore found between T0 and T2I, and there are 12 sets in the Tn/TnI equivalence class (Rahn 1980, 148). See alsoReferences
Further reading
External links
| |
This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Set_theory". Allthough most Wikipedia articles provide accurate information accuracy can not be guaranteed. |
Help us with donations or by making music available!
©2023 Classic Cat - the classical music directory

Mozart, W.A.
Piano Sonata no. 3 in B flat major KV281
Jacqueline Blancard
Copland, A.
Old American Songs set 1
Fountain Valley High School
Mozart, W.A.
Eine kleine Nachtmusik (serenade no. 13)
Orchestre Nationale de France
Tchaikovsky, P.I.
The Seasons
Alfonso Bertazzi
Brahms, J.
Violin Sonata No. 2 in A Major
Washington Musica Viva
Rachmaninov, S.
Rhapsody on a Theme of Paganini
Dimitris Sgouros

 to denote ordered sequences (Rahn 1980, 21 & 134), while others distinguish ordered sets by separating the numbers with spaces (Forte 1973, 60–61). Thus one might notate the unordered set of pitch classes 0, 1, and 2 (e.g., C, C
to denote ordered sequences (Rahn 1980, 21 & 134), while others distinguish ordered sets by separating the numbers with spaces (Forte 1973, 60–61). Thus one might notate the unordered set of pitch classes 0, 1, and 2 (e.g., C, C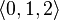 or (0,1,2). C is not always considered to be zero; for example, a piece (whether tonal or atonal) with a clear pitch center of F might be most usefully analyzed with F set to zero (in which case {0,1,2} would represent F, F
or (0,1,2). C is not always considered to be zero; for example, a piece (whether tonal or atonal) with a clear pitch center of F might be most usefully analyzed with F set to zero (in which case {0,1,2} would represent F, F